 ADSORPTION:
ADSORPTION:Energy distribution function
(Used in General Integral Equation of Adsorption)
© A.W.Marczewski 2002
A Practical Guide to Isotherms of ADSORPTION on Heterogeneous Surfaces
 ADSORPTION:
ADSORPTION:
Energy distribution function
(Used in General Integral Equation of Adsorption)
Page under reconstruction
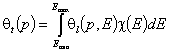 General Integral Equation of Adsorption (GIEA) is a general formulation of adsorption isotherm involving energetic heterogeneity of the adsorption system (i.e. adsorbate-surface).
General Integral Equation of Adsorption (GIEA) is a general formulation of adsorption isotherm involving energetic heterogeneity of the adsorption system (i.e. adsorbate-surface).
CAUTION!
One has to be always cautious while describing energy distribution function as the property of adsorbent only. Though for homogeneous adsorbents it may be true, it may change not only with the change of such adsorbate properties like functional groups, but also with changing molecular size and shape and surface topography (see also below). Moreover, in adsorption of mixtures the obtained energy distribution function may have altered - and quite different - shape and width depending on energy correlations for molecule pairs on adsorption sites.
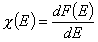
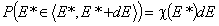 Differential Energy Distribution Function χ(E)
Differential Energy Distribution Function χ(E)
Global (overall) isotherm of adsorption θt is obtained by averaging of local adsorption coverage θt (adsorption energy dependent) corresponding to adsorption on various surface sites. This local isotherm equation describes adsorption on energetically homogeneous surface, however the weight factor is a non-negative differential energy distribution function χ(E) giving relative frequencies (probabilities) of surface sites characterized by some adsorption energy for a given adsorbate (see below).
For homogeneous surface (Langmuir isotherm) this function is defined as the Dirac's delta (impulse)
function.
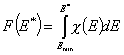
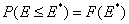 Integral (cumulative) Energy Distribution Function F(E)
Integral (cumulative) Energy Distribution Function F(E)
The differential energy distribution χ(E) function is defined as the probability density function of adsorption energy. The General Integral Equation of Adsorption may be easily reformulated in a way allowing for use of integral (cumulative) energy distribution function F(E) instead of differential function χ(E).
For homogeneous surface (Langmuir isotherm) this function becomes a simple stepwise function (Heaviside step function) equal to zero for energies less than charactersitic adsorption energy and equal to 1 for energies greater than or equal to this energy value (alternative definition).
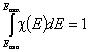
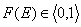 Normalization of Energy Distribution Function
Normalization of Energy Distribution Function
The values of F(E) are always between 0 and 1, whereas the integral of χ(E) over energy E is normalized to 1. Such normalization approach simplifies formulation of generally applied equation, however, if needed such normalization conditions (integral = 1 and 0 to 1 range, correspondingly) may be redefined. If the General Integral Equation of Adsorption is reformulated by replacing relative coverages (θ) by actual adsorbed amounts, then in the above normalization conditions we must replace dimensionless 1 (corresponding to the monolayer capacity) by maximum adsorption capacity (in the monolayer!), am expressed in e.g. [mmol/g].
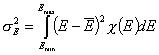
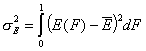 Dispersion of Adsorption Energy
Dispersion of Adsorption Energy
Besides energy distribution general shape and symmetry an important parameter of energy distribution function is its energy dispersion (or - in general meaning - distribution width). This factor decides whether energetic heterogeneity effects will be visible in isotherm's behavior. For energy distributions of low energy dispersion the behavior of isotherm at moderate coverages will resemble Langmuir isotherm. If energy dispersion is high, the sensitivity of adsorption to the changes of pressure (or concentration) at moderate coverages will be much weaker than in the case of Langmuir isotherm (will resemble the middle section of Generalized Freundlich, Langmuir-Freundlich, Tóth etc. isotherm)
Henry behavior
If the distribution has finite width (i.e. has minimum and maximum energy) or it behaves in a special way at low and high adsorption energies the corresponding isotherm should display a so-called Henry and Langmuir behavior for low and high coverages, respectively.
Surface site topography and lateral interactions - local isotherm:
On random topography surfaces the interaction factor* depends on the mean field of adsorbate molecules which is surface-averaged anyway, i.e. it depends on the local average adsorbate density which is the same as average density of adsorbate molecules over the whole surface (that is: θl,avg = θt) and thus does not depend on which particular site the molecule is sitting (i.e. does not depend on local adsorption energy E).
However, for patchwise topography, the density of adsorbate molecules is characteristic - and different (depending on the local adsorbate density, i.e. local coverage θl) - for each of the patches characterized with different adsorption energy E.
* (Interacton factor describes how the presence of other adsorbate molecules affects adsorption forces by attractive Van der Waals forces, by specicic forrces like associative or hydrogen bonding, or by electrostatic forces - see expressions for Kiselev and Fowler-Guggengeim in gas and solute adsorption)
Global isotherm and surface topography
If for a given type of heterogeneity and without lateral interactions present the isotherm equation θt(c) (or for gas adsorption: θt(p)) has analytical form, it will be analytical with lateral interactions and random site topography, too. New isotherm θt,int(c) (or θt,int(p)) will have indentical form as the original equation if we replace concentration (or pressure for gas adsorption) by a suitable term c' = c f(θt) (or p' = p f(θt)).
For patchwise topography with lateral interactions the obtained isotherms are generally non-analytical.
Model pictures
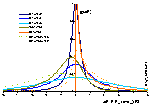
Comparison of differential and integral (cumulative) energy distribution functions
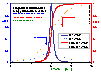 Comparison of χ(E) and F(E)
Comparison of χ(E) and F(E)
Differential energy distribution function χ(E) (blue lines; area under curve is 1) and corresponding integral distribution F(E) (red/orange lines; Fmin=0, Fmax=1) for LF isotherm (m=n= 0.9 and 0.5), E=ε/RT - reduced energy.
 Comparison of χ(z) and F(z)
Comparison of χ(z) and F(z)
Differential energy distribution function χ(z) (blue lines; area under curve is 1) and corresponding integral distribution F(z) (red/orange lines; Fmin=0, Fmax=1) for LF isotherm (m=n= 0.9 and 0.5), z(F)=E(F)-Eo - relative energy (E=ε/RT - reduced energy).
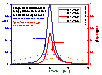 Differential energy distribution χ(E) and surface coverage, local θl and global θl
Differential energy distribution χ(E) and surface coverage, local θl and global θl
Differential energy distribution functions χ(E) (blue lines; area under curve is 1) and products of local coverage and energy distribution function θl(p,E)χ(E) (red/orange lines; area under curve is equal to global/overall coverage θt(p)) for LF isotherm (m=n= 0.9 and 0.5, fixed pressure, Kp=1).
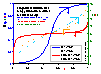 Influence of heterogeneity
Influence of heterogeneity
Influence of heterogeneity on energy distribution E(F) (red/orange lines; function inverse to integral (cumulative) energy distribution) and local coverage θl(p,E(F)) (blue lines; areas under curves are equal to global/overall coverages, θ(p)) for LF energy distribution.
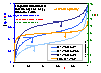 Influence of pressure (low heterogeneity)
Influence of pressure (low heterogeneity)
Influence of pressure on local coverage θl(p,E(F)) (blue lines; areas under curves are equal to global/overall coverages, θ(p)) for LF energy distribution (energy distribution E(F) - orange line; function inverse to integral (cumulative) energy distribution) (low heterogeneity).
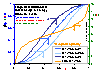 Influence of pressure (high heterogeneity)
Influence of pressure (high heterogeneity)
Influence of pressure on local coverage θl(p,E(F)) (blue lines; areas under curves are equal to global/overall coverages, θ(p)) for LF energy distribution (energy distribution E(F) - orange line; function inverse to integral (cumulative) energy distribution) (high heterogeneity).
Top
My papers
Search for papers
Main page
Send a message to Adam.Marczewski AT@AT umcs.lublin.pl