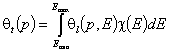 General Integral Equation of Adsorption
General Integral Equation of Adsorption© A.W.Marczewski 2002
A Practical Guide to Isotherms of ADSORPTION on Heterogeneous Surfaces
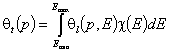 General Integral Equation of Adsorption
General Integral Equation of Adsorption
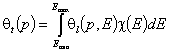 - for single gas adsorption
- for single gas adsorption
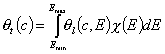 - for dilute single-solute adsorption
- for dilute single-solute adsorption
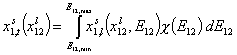 - for binary liquid adsorption
- for binary liquid adsorption
Local isotherm equation θl
Local isotherm equation (usually Langmuir isotherm for gas or dilute solute adsorption, BET for vapor adsorption and Everett for liquid mixture adsorption) corresponds to adsorption on homogeneous (i.e. energetically non-heterogeneous) surface.
This local isotherm equation has always a term dependent on energy of adsorption ε (gas or vapor) or on a difference of adsorption energies of adsorbing molecules (or energy related to exchange of molecules) in liquid mixtures (or in gas mixtures at very high pressures when practically all surface sites are occupied). However, how this adsorption energy affects isoterm it depends also on temperature as all energy terms are always present as energy/RT terms. So it is better to use a so-called reduced energy, E:
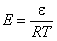 - reduced energy
- reduced energy
In dilute solutions we usually talk about energy of adsorption of some molecule treating it like gas adsorption, while in fact it is always a difference of adsorption energies of a solute and solvent molecule (often water). This simplification is valid only if solvent concentration remains constant.
This local isotherm equation may in general include various terms, like lateral interactions (specific and non-specific) and multilayer formation (see gas or solute adsorption). If lateral interactions are involved then the spatial distribution (surface topography) of adsorption sites is important.
For gas and solute adsorption the most common local isotherm is the Langmuir equation:
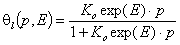 - Langmuir eq., gas adsorption
- Langmuir eq., gas adsorption
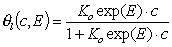 - Langmuir eq., solute adsorption.
- Langmuir eq., solute adsorption.
For adsorption in liquid mixtures, the most common local isotherm is the Everett isotherm, which may be represented (the "competitive form") as:
 - Everett eq., liquid ads.
- Everett eq., liquid ads.
where:
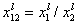 - ratio of molar fractions
- ratio of molar fractions
and
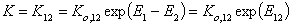 - equilibrium constant
- equilibrium constant
Another often used - and more general - isotherm is the equation obtained in the regular solution theory.
Global (overall) isotherm of adsorption θt
Global (overall) isotherm of adsorption θt (i.e. relative surface coverage = (adsorbed amount) / (maximum amount adsorbed in monolayer)) is obtained by averaging of local coverage θt (adsorption energy dependent isotherm equation) corresponding to adsorption on energetically homogeneous surface. This averaging depends on the site's relative frequency or probability.
 Differential energy distribution function χ(E)
Differential energy distribution function χ(E)
Integral (cumulative) energy distribution function F(E)
The non-negative differential energy distribution function χ(E) gives relative frequencies (probabilities, P) of surface sites characterized by a some adsorption energy for a given adsorbate. This differential energy distribution χ(E) function is defined as the probability density function of adsorption energy:
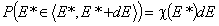
This equation may be easily reformulated in a way allowing for use of integral (cumulative) energy distribution function F(E):
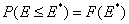
and following that we have:
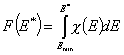 and
and
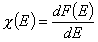
Normalization of energy distribution functions.
The integral of differential energy distribution function χ(E) over energy E is normalized to 1:
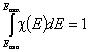 - normalization of χ(E)
- normalization of χ(E)
whereas the values of integral energy distribution functions F(E) are always between 0 and 1 (probability, always in <0,1> range):
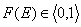 and
and
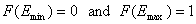
For a homogeneous surface (e.g. Langmuir isotherm):
χ(E) is defined as the Dirac's delta (impulse) function, δD(E), which is equal to 0 everywhere but in some fixed point - in this case E=Eo average and characteristic energy - and is normalized to 1; F(E) is a simple Heaviside (step) function, F(E) = 0 for E<Eo and F(E) = 1 for E≥Eo (this step function may be also defined alternately).
General Integral Equation of adsorption - redefined with integral (cumulative) energy distribution function F(E):
(This formulation makes it much easier to describe and analyze adsorption in multicomponent adsorption systems - see my references 1 and 2)
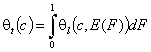 - gas and vapor adsorption
- gas and vapor adsorption
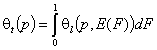 - single solute adsorption
- single solute adsorption
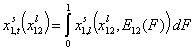 - binary liquid mixtures
- binary liquid mixtures
Mean (average) energy and shape of energy distribution function
One of the main factors in adsorption in the average adsorption energy (or position of distrbution function on energy axis):
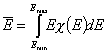 and
and
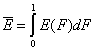
Dispersion of adsorption energy
The second factor is the width of energy distribution, which tells in a general way how much the adsorption sites are different by their adsorption energy. The most general way to compare widths of distribution functions is by comparing their energy dispersions. The definition of energy dispersion, σ, does not depend on definition of a particular distribution function (i.e. function shape, like Gauss bell-curve, continuous/Square/UNILAN, quasi-gaussian LF or Rudzinski, asymmetrical GF or Tóth etc.):
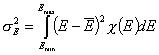 or
or
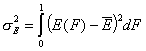
The magnitude of energy dispersion decides whether energetic heterogeneity effects will be visible in isotherm's behavior.
Henry behavior
Besides average adsorption energy and energy dispersion (or distribution width) the general shape and symmetry of energy distribution function the behavior of such function at low and high adsorption energies is very important. It affects the behavior of isotherm at very high and respectively very low pressures (concentrations) - see Henry and Langmuir behavior for low and high coverages, respectively.
Separation of magnitude of adsorption energy and energy distribution shape
(see my references 1 and 2)
By rearrangement of equations and some simple definitions we may separate effects corresponding to the magnitude of adsorption energy (average adsorption energy, i.e. position of energy distribution function on the energy axis) from the general shape of energy distribution function (width or dispersion of energy distribution function). Other important parameters like minimum and maximum energy will be defined with those already defined parameters. This approach makes it easier to describe and analyse adsorption on energetically heterogeneous solids, especially in multicomponent adsorption systems.
First let us define the relative adsorption energy z=E-Eo where Eo is some characteristic adsorption energy (e.g. minimum adsorption energy for GF isotherm or average adsorption energy for symmetrical energy distributions like Gauss, LF, Rudzinski etc.):
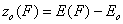 - relative energy (relative vs. characteristic energy)
- relative energy (relative vs. characteristic energy)
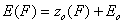 - energy
- energy
For the sake of this summary I will use average energy marked with upper dash:
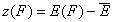 - relative energy (relative vs. average energy)
- relative energy (relative vs. average energy)
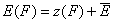 - energy
- energy
 Then we obtain energy distribution functions that define only the shape of the energy distribution, while the position (with minimum, maximum and average or characteristic energies) is defined by the characteristic or average energy:
Then we obtain energy distribution functions that define only the shape of the energy distribution, while the position (with minimum, maximum and average or characteristic energies) is defined by the characteristic or average energy:
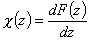 - differential relative energy distribution function
- differential relative energy distribution function
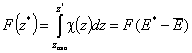 - differential relative energy distribution function
- differential relative energy distribution function
If we calculate the average of relative energy function (defined relative vs. average adsorption energy), we will obtain 0 by definition:
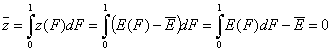
(For the z(F) definition relative vs. characteristic energy Eo, i.e. zo(F), we will get the characteristic energy minus average energy)
The energy dispersion will be then calculated as:
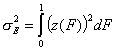
General Integral Equation of Adsorption - reformulated with relative adsorption energy functions z(F):
Finally we will obtain reformulated General Integral Equation of Adsorption:
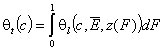 - gas and vapor phase
- gas and vapor phase
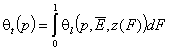 - dilute single solute
- dilute single solute
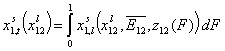 - binary liquid mixture
- binary liquid mixture
In these equations the average (or characteristic) adsorption energy enters the expression for adsorption equilibrium constant K of the local isotherm equation θl. Then the relative energy term z(F) corresponds only to the relative changes of the local equilibrium constant.
For the relative energy term zo(F) defined for the characteristic energy, Eo, we have:
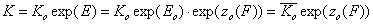 - relative vs. characteristic energy
- relative vs. characteristic energy
whereas for the relative energy term z(F) defined as relative to the average adsorption energy (default characteristic energy), we get:
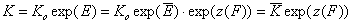 - relative vs. average energy
- relative vs. average energy
For a homogeneous surface (e.g. Langmuir isotherm):
χ(z) is defined as the Dirac's delta (impulse) function, δD(z), which is equal to 0 everywhere but in some fixed point - in this case z=0 - and is normalized to 1; F(z) is a simple Heaviside (step) function, F(z) = 0 for z<0 and F(z) = 1 for z≥0 (this step function may be also defined alternately).
Adsorption energy - property of the entire system
One has to be always cautious while describing energy distribution function as the property of adsorbent only. Though for homogeneous adsorbents it may be true, it may change not only with the change of such adsorbate properties like functional groups, but also with changing molecular size and shape and surface topography. Moreover, in adsorption of mixtures the obtained energy distribution function may have altered - and quite different - shape and width depending on energy correlations for molecule pairs on adsorption sites.
Surface site topography and lateral interactions - local isotherm:
On random topography surfaces the interaction factor depends on the mean field of adsorbate molecules which is surface-averaged anyway, i.e. it depends on the local average adsorbate density which is the same as average density of adsorbate molecules over the whole surface (that is: θl = θt) and thus does not depend on which particular site the molecule is sitting (i.e. does not depend on local adsorption energy E).
However, for patchwise topography, the density of adsorbate molecules is characteristic - and different (depending on the local adsorbate density, i.e. local coverage θl) - for each of the patches characterized with different adsorption energy E.
Global isotherm and surface topography
If for a given type of heterogeneity and without lateral interactions present the isotherm equation θt(c) (or for gas adsorption: θt(p)) has analytical form, it will be analytical with lateral interactions and random site topography, too. New isotherm θt,int(c) (or θt,int(p)) will have indentical form as the original equation if we replace concentration (or pressure for gas adsorption) by a suitable term c' = c f(θt) (or p' = p f(θt)).
For patchwise topography with lateral interactions the obtained isotherms are generally non-analytical.
Global/overall multilayer isotherm (gas or dilute solute adsorption)
May be easily obtained from its monolayer form, see for gas and vapor and solute adsorption.
Top
My papers
Search for papers
Main page
Send a message to Adam.Marczewski AT@AT umcs.lublin.pl