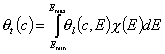Monolayer (flat surface) localized adsorption on energetically heterogeneous surfaces (local isotherm - Langmuir):
All those equations are based on so called General Integral Equation and may include lateral interactions (of FG, simplified Kiselev and full Kiselev type - see local isotherms and derivation) or multilayer formation (BET - see other isotherms below or general formulation).
-
GL - Generalized Langmuir (aka. MJ, M-J: Marczewski-Jaroniec) is a combination of Langmuir local isotherm with surface heterogeneity controlled by 2 parameters (0 ≤ m,n ≤ 1), for specific parameter values this equation reduces to Langmuir (L)(homogeneous), Generalized Freundlich (GF)/Sips, Langmuir-Freundlich (LF) and Tóth (T) isotherms.
- GF - Generalized Freudlich (aka. Sips eq.) (GL with n=1) - exponentially decreasing distribution of ads. energy, but in contrast to the "true Freundlich" - monolayer; reduces to Freundlich eq. for low adsorption values - does not show Henry behaviour at low conc.
- LF - Langmuir-Freundlich (GL with m=n) - symmetrical quasi-gaussian energy distribution (reduces to Freundlich eq. for low adsorption values; does not show Henry behaviour for low conc.)
- T - Tóth (GL with m=1) - asymmetrical quasi-gaussian energy distribution with strong tail for low adsorption energies (reduces to Henry isotherm (a=Kc) for low adsorption values)
- Sq - "Square" (aka. UNILAN) - monolayer physical adsorption with continuous (constant) energy distribution of ΔE width. Displays Henry behaviour (a=Kc) for low conc. (or pressures); for coverages close to 0.5 similar to LF and Gauss; related to a non-monolayer Tiemkin eq. ( below ).
- G - "Gauss" - monolayer physical adsorption with (true) Gaussian energy distribution of σ dispersion; no analytical isotherm equation exists. Displays Henry behaviour (a=Kc) for low very conc. (or pressures); for coverages close to 0.5 similar to LF, Sq etc. with similar energy dispersion.
- R - Rudzinski - monolayer physical adsorption with simple symmetrical quasi-gaussian energy distribution; no analytical isotherm equation exists but this isotherm is very similar to LF. Does not display Henry behaviour at low conc.
All isotherms follow Henry behaviour at very low concentrations or pressures, like other isotherms without heterogeneity effects.
- Localized adsorption:
- L - Langmuir eq. - monolayer localized physical adsorption on homogeneous surface; may be extended with heterogeneity effects, lateral interactions and multilayer effects
-
FG - Fowler-Guggenheim eq. - localized physical adsorption with non-specific lateral interactions (mean-field approx.) on homogeneous surface (gas phase), may be extended with heterogeneity effects. It reduces to Langmuir isotherm in absence of lateral interactions.
Identical in form equation is known as Frumkin isotherm and used in electrochemistry (e.g. adsorption of ions on mercury etc.) - Kis - simplified Kiselev eq. - localized physical adsorption with specific lateral interactions (associative) on homogeneous surface (gas phase), in full form it combines FG non-specific (mean-field) lateral interactions with specific (associative) ones. It may be extended with heterogeneity effects. Reduces to Langmuir isotherm in absence of lateral interactions.
- Jov - Jovanovic eq. - unlike L, FG or Kiselev it considers vertical interactions bulk/surface phase (derived from kinetic considerations, however, no proper statistical-mechanics derivation exists); homogeneous but may be extended with heterogeneity effects (see e.g. JF/Jov-m). Does not reduce to Langmuir isotherm.
- Mobile adsorption:
(Partially mobile models are known but eqns. are much more complicated.) Should be used for gases and vapors not for liquids.
- Volmer - Volmer eq. - mobile physical gas adsorption on homogeneous surface (gas phase), may be extended with heterogeneity effects.
- HB - Hill-de Boer eq. - mobile physical gas adsorption with FG-like (mean-field) lateral interactions on homogeneous surface (gas phase), may be extended with heterogeneity effects.
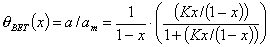Multilayer isotherms (reduced concentration: x = c/cs or reduced pressure: x = p/ps) - most based on BET equation (all reduce to Langmuir isotherm at lower relative concentrations x=c/cs or pressures x = p/ps and display Henry behaviour for very low x → 0; all those equations may also serve as local isotherms in General Integral Equation of Adsorption involving energetic heterogeneity effects):
- Brunauer-Emmett-Teller (BET) - 2-parameter equation for infinite no. of layers (on flat surface only) - predicts always too big multilayer adsorption. For a finite no. of layers (e.g. in a pore) a 3-parameter n-layer BET equation is obtained (see its classic form) (Note: actual max. statistical multilayer thickness for n-layer BET is not n but: 1+(n-1)/2). Another n-layer isotherm is a 4-parameter BDDT (Brunauer-Deming-Deming-Teller) equation.
- Hüttig - 2-parameter equation - predicted adsorption is always smaller than for BET
- Sircar - 3-parameter equation
- Lopez-Gonzalez & Dietz (LGD) - 2-parameter equation - average of BET and Hüttig, may be also approximated by a simpler LGDa equation given by AWM.
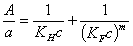Other experimental isotherms:
Not limited by monolayer capacity; may show maximum adsorption for dilute solutions of weakly soluble substances or vapours because of concentration/pressure limit
-
F - Freundlich equation (see also below).
GL equation may reduce to F for low adsorption values for specific values of heterogeneity parameters (e.g. specifically LF,GF). Very often used (with success) to describe adsorption in a narrow or moderately large adsorption range (for strongly heterogeneous or microporous solids, e.g. active carbons, it may translate into a quite large concentration range) -
RP - Redlich-Peterson (invented) a.k.a. Radke-Prasunitz (popularized):
for low adsorptions similar to Henry (a=Kc) isotherm, for medium and high adsorptions behaves like Freundlich eq. (a=(Kc)m) (it may be considered as a harmonic combination of Henry and Freundlich equations).
This equation is even more successful than Freudlich (above) in practical description of experimental data. - Jos - Jossens eq. (experimental; exponential dependence of isosteric heat of adsorption on adsorption)
- Tiemkin (Temkin, Tiomkin) - Tiemkin eq. - experimental - used predominantly in gas catalysis; strong heterogeneity with constant energy distribution (continuous from -∞ to +∞; may be treated as a simplification of ( above ) Sq aka. UNILAN isotherm, but only far from monolayer filling region).
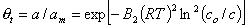Adsorption in micropores (maximum adsorption capacity is analogous to monolayer capacity):
Based on the Theory of Pore Volume Filling by Dubinin and Radushkevich
- F - Freundlich equation (DA with n=1)
- DR - Dubinin-Raduskevich (DA with n=2)
- DA - Dubinin-Astakhov (usually n=3)
- DRS,DS - Dubinin-(Radushevich)-Stoeckli - obtained form Stoeckli eq.
- Stoeckli - non-analytical solutions of Stoeckli integral equation with DR serving as local isotherm
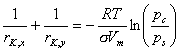Adsorption in mesopores (usually N2 adsorption):
Adsorption is a combination of adsorption on mesopore walls with condensation of adsorbate in pores, where meniscus reached a critical radius. Generally such isotherms display hysteresis loops (adsorption and desorption go along different paths) in the mesopore region (x = p/ps ≥ 0.40 for N2 and x ≥ 0.175 - 0.98 for benzene). It is assumed that in this "mesopore" range all micropores are filled and monolayer is filled, too.
Methods of data analysis use meniscus radius calculated from Kelvin equation and statistical layer thickness of adsorbate (often given by Harkins-Jura (HJ) or by Halsey / Frenkel-Halsey-Hill (FHH) eq. with specific expressions for N2 adsorption: tHJ and tHalsey, respectively - see also above) in order to find pore diameter.
- Calculations depend on a mesopore shape:
- cylindrical mesopores (Kelvin eq. with ry=+∞)
- spherical mesopores (Kelvin eq. with rx=ry)
- slit-shaped mesopores
- other like bottle-shaped pores
- Mesopore filling model / pore distribution calculation scheme:
- Barret-Joyner-Halenda (BJH)
- simplified BJH
- Dubinin (like BJH, but takes into account the dependence of N2 surface tension on meniscus radius)
- Density-Functional Theory (DFT)
