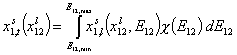 General Integral Equation of Adsorption:
General Integral Equation of Adsorption:Binary liquid mixtures
© A.W.Marczewski 2002
A Practical Guide to Isotherms of ADSORPTION on Heterogeneous Surfaces
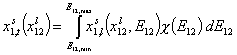 General Integral Equation of Adsorption:
General Integral Equation of Adsorption:
Binary liquid mixtures
see G.I.E.A. for dilute solute and gas adsorption
see G.I.E.A. for multicomponent adsorption
isotherm equations |
GL isotherm
GL energy distribution |
energy dispersion |
Global Heterogeneity
NOTE
Equations below are good for binary liquid mixtures. If you deal with partially miscible solutions this equations must be modified. Dilute single-solute adsorption is a special case of binary liquid mixture adsorption where one of the components (solvent) is present in the solution bulk in almost constant concentration.
General Integral Equation of Adsorption (GIE) is a general formulation of adsorption isotherm involving energetical heterogeneity of the adsorption system (i.e. adsorbate-surface). (One has to be always aware that in the case of mixtures the observed adsorption effect is always an exchange of 2 or more molecules - i.e. adsorption in solutions is always a competitive phenomenon).
The first attempt to describe adsorption on non-homogeneous solids was by Langmuir (1918) but it was represented by a simple summation not an integral.
Another similar in character Integral Equation of Adsorption is the Stoeckli integral equation for adsorption on microporous non-uniform solids.
General Integral Equation of Adsorption
For binary liquid adsorption:
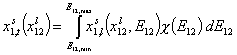
where: xi is molar fraction of component "i", xs is molar fraction in surface phase and xl is molar fraction in bulk phase, xsi,t is global (overall) molar fraction of component "i" and xsi,l is local molar fraction of component "i" (in surface phase). xij = xi/xj and Eij = Ei-Ej is the difference of adsorption energies corresponding to the exchange of component "j" for "i" on a given site (competitive adsorption).
Energy distribution function
see also:
a section in General Integral Equation of Adsorption (simple cases)
General Integral Equation of Adsorption (multicomponent)
Energy correlation (competition of components)
Adsorption basics (gas vs. liquid adsorption)
CAUTION!
One has to be always cautious while describing energy distribution function as the property of adsorbent only. Though for homogeneous adsorbents it may be true, it may change not only with the change of such adsorbate properties like functional groups, but also with changing molecular size, shape and surface topography. Moreover, in adsorption of mixtures the obtained energy distribution function may have altered - and quite different - shape and width depending on energy correlations for molecule pairs on adsorption sites.
Monolayer
Local Everett isotherm:
Localised monolayer physical adsorption:
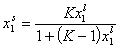 - Everett equation (original form)
- Everett equation (original form)
 - Everett equation (rearranged form)
- Everett equation (rearranged form)
where:
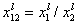 and
and
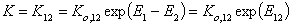
and where: Ko,12 is entropy-related and temperature dependent constant (so-called pre-exponential factor), sites are characterised by the difference of reduced adsorption energies E12 (or rather reduced energies of adsorption of molecules "1" and "2" on certain site are E1 and E2, respectively).
The global isotherms θt(xl12) will have identical mathematical form as the isotherms in gas phase θt(p) or dilute solutions θt(c) provided that distribution of energy differences χ(E12) in binary mixture is the same as the corresponding distribution of adsorption energy χ(E) for gas adsorption or dilute single-solute adsorption.
General Integral Equation | Monolayer ( Local isotherm )
Top
My papers
Search for papers
Main page
Send a message to Adam.Marczewski AT@AT umcs.lublin.pl