© A.W.Marczewski 2002
A Practical Guide to Isotherms of ADSORPTION on Heterogeneous Surfaces
Reload Adsorption Guide
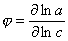 ADSORPTION: φ-function
ADSORPTION: φ-function
General Integral Equation /
GL (Generalized Langmuir) /
All equations (preview)
Adsorption type (
Linear Langmuir plot /
Graham plot /
Consistency /
Henry constant )
Popular isotherms
(
Mono-,
Multilayer,
Experimental,
Micro-,
Mesoporous
)
Data analysis: (
LSq data fitting /
Global heterogeneity /
Linear plots /
φ-function
)
Prediction/Description of
Multicomponent adsorption /
Wastewater adsorption
Heterogeneity and Molecular Size ( Theory and Prediction / Simple binary isotherm )
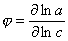 φ-function method:
φ-function method:
Use a so-called:
φ-function method (where
φ = δ log(a)/
δ log(c)) (derivative of adsorption isotherm in logarithmic co-ordinates).
- A.W. Marczewski, M. Jaroniec, Mh. Chem, 114, 711, (1983),
(doi).
- M. Jaroniec, A.W. Marczewski, Mh. Chem. 115, 997 (1984),
(doi).
- M. Jaroniec, A.W. Marczewski, Mh. Chem. 115, 1013 (1984),
(doi).
- M. Jaroniec, A.W. Marczewski, J. Colloid Interface Sci., 101, 280 (1984),
(doi).
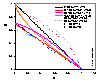 φ-function is a dimensionless variable (independent of adsorption and concentration/pressure units as well as independent of type of logarithm you use). Various plots of φ-function versus adsorption, pressure/concentration etc. allow to determine isotherm type and isotherm parameters (or sometimes at least to reject some existing choices)
(Here are model pictures)
φ-function is a dimensionless variable (independent of adsorption and concentration/pressure units as well as independent of type of logarithm you use). Various plots of φ-function versus adsorption, pressure/concentration etc. allow to determine isotherm type and isotherm parameters (or sometimes at least to reject some existing choices)
(Here are model pictures)
NOTE. This method allows to determine equation type and parameters very precisely, however your data should be very good - evenly spaced, smooth and in a wide range of relative adsorption φ) - method is sensitive to data scatter.
-
for Langmuir (L) and Langmuir-Freundlich (LF) isotherms:
( φ = m / [1 + (Kc)m] = m [1 - θ] )
(special case is Langmuir, m=1) a simple dependence of φ vs. a is obtained
-
for Generalized Langmuir (GL) isotherm
( φ = m / [1 + (Kc)n] = m [1 - θn/m] )
in order to obtain simple linear dependences involving only experimental data (e.g. φ, a, c) calculation of 2nd derivative would be required. In such a case method becomes much more sensitive to experimental data scatter.
-
for Generalized Langmuir with FG lateral interactions (GL-FG) isotherm
( φ = m [1 - θn/m] / {1 - mαθ [1 - θn/m]} )
where α is lateral interaction coefficient.
-
Radke-Prausnitz aka. Redlich-Peterson (RP)
( φ = 1 - n {(Kc)n / [1 + (Kc)n]} )
(3-step method):
- determine parameter m from linear dependence 1-φ vs. a/c
1 - φ = m - (m/amK)(a/c)
- determine parameter product amK from linear dependence (a/c) vs. (a/c)cm
(a/c) = amK - Km [(a/c)cm]
- determine parameter K and am from linear dependence (c/a) vs. (cm) (amK and m are already estimated).
(c/a) = 1/(amK) - Km/(amK) (cm)
-
Jossens
( φ = 1 / [1 + b m am] = 1 / [1 + m ln(Kc/a)] )
(2-step to 3-step method):
- determine parameter m from linear dependence (1/φ - 1) vs. ln(a/c)
(1/φ - 1) = m ln(K) - m ln(a/c)
- determine parameters b and K from linear dependence ln(a/c) vs. am
ln(a/c) = ln(K) - b (am)
- improve K-value by using one of dependencies (use earlier obtained m and b):
- determine parameter K from linear dependence (a/c) vs. exp(-b am)
(a/c) = K exp(-b am)
- determine parameter K from linear dependence (c/a) vs. exp(b am)
(c/a) = K exp(b am)
-
linear dependence (approximate!): φ vs. ln(a)
It corresponds to φ = n [ln(am) - ln(a)] or isotherm equation: a = am exp(-A/cn). This isotherm does not reduce to Henry isotherm for low concentrations and is not consistent with local Langmuir behaviour, however it may be treated as an approximation of GL equation for high adsorption values (close to monolayer) especially if strong lateral interactions are also involved (e.g. GL-FG). Then estimated parameters ( n = nGL, am = am,GL and A = mGL/(n Kn) ) may be used in GL equation.
-
for Jovanovic and Jovanovic-Freundlich (JF/Jov-m) isotherms
( φ = m (Kc)m / {exp[(Kc)m] - 1} = m [(1-θ)/θ] [ -ln (1-θ)] )
linear dependences are difficult to use (at least am is required in order to calculate θ):
- estimate m from: φ vs. [(1-θ)/θ] [ -ln(1-θ)]
φ = m [(1-θ)/θ] [ -ln(1-θ)]
much better idea is to use simple linear relationship not involving φ - both m and K are determined in one step (am is still required)
-
Freundlich (F or DA with n=1): φ = const (and equal to B1RT = m ).
-
Dubinin-Radushkevich (DR or DA with n=2), linear dependences:
-
estimate ln(co) (and B2(RT)2) from: φ vs. ln(c)
φ = [2B2(RT)2] [ln(co) - ln(c)]
-
estimate ln(am) (and B2(RT)2) from: φ2 vs. ln(a)
φ2 = [4B2(RT)2]2 [ln(am) - ln(a)]
-
Dubinin-Astakhov (DA; n must be known in advance) linear dependences:
- estimate ln(co) (and Bn(RT)n) from: φ1/(n-1) vs. ln(c)
φ1/(n-1) = [n Bn(RT)n]1/(n-1) [ln(co) - ln(c)]
- estimate ln(am) (and Bn(RT)n) from: φn/(n-1) vs. ln(a)
φn/(n-1) = [nn Bn(RT)n]1/(n-1) [ln(am) - ln(a)]
Adsorption type (
Linear Langmuir plot /
Graham plot /
Consistency /
Henry constant )
Popular isotherms
(
Mono-,
Multilayer,
Experimental,
Micro-,
Mesoporous
)
Data analysis: (
LSq data fitting /
Global heterogeneity /
Linear plots /
φ-function
)
Prediction/Description of
Multicomponent adsorption /
Wastewater adsorption
Heterogeneity and Molecular Size ( Theory and Prediction / Simple binary isotherm )
General Integral Equation /
GL (Generalized Langmuir) /
All equations (preview)
Top
My papers
Search for papers
Main page
E-mail addresses are modified to in order to prevent spamming / mail-abuse:
in e-mail remove spaces, replace " AT@AT " by "@"
Send a message to Adam.Marczewski AT@AT umcs.lublin.pl
Disclaimer
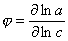 ADSORPTION: φ-function
ADSORPTION: φ-function
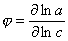 ADSORPTION: φ-function
ADSORPTION: φ-function
 φ-function is a dimensionless variable (independent of adsorption and concentration/pressure units as well as independent of type of logarithm you use). Various plots of φ-function versus adsorption, pressure/concentration etc. allow to determine isotherm type and isotherm parameters (or sometimes at least to reject some existing choices)
(Here are model pictures)
φ-function is a dimensionless variable (independent of adsorption and concentration/pressure units as well as independent of type of logarithm you use). Various plots of φ-function versus adsorption, pressure/concentration etc. allow to determine isotherm type and isotherm parameters (or sometimes at least to reject some existing choices)
(Here are model pictures)