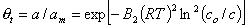 Isotherms of Micropore Filling Theory
Isotherms of Micropore Filling Theory
© A.W.Marczewski 2002
A Practical Guide to Isotherms of ADSORPTION on Heterogeneous Surfaces
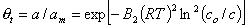 Isotherms of Micropore Filling Theory
Isotherms of Micropore Filling Theory
NOTE
Characteristic micropore-filling concentration co is smaller than cs (concentration of saturated solution). Analogously, for vapours, po < ps.
Micropore - pore with diameter below ca. 2 nm (larger pores are mesopores, 2-50nm - IUPAC - or sometimes 2-100 nm). Large micropores are often called supemicropores.
The adsorption process in micropores is much stronger than on relatively flat surfaces of meso- and macropores. The adsorbate molecule in micropore is closely surrounded by pore walls. Due to force - distance characteristics of adsorption forces (for dispersive attraction forces of a molecule near flat solid surface, F(r) ∝ 1/r3 ) in small pores the adsorbate interacts with larger number of solid wall atoms, as compared to larger pores, where closeness to one of walls means much weaker interactions with other walls.
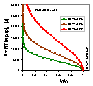 The Micropore Volume Filling Theory was proposed by Dubinin-Radushkevich and co-workers for adsorption from gas phase. It is related to Eucken/Polany'i potential theory (characteristic adsorption potential curve a = f(A) , where a is adsorption and A = RT ln(ps/p) is adsorption potential, and A=0 at saturation point; analogously, in solutions: A = RT ln(cs/c) ).
The Micropore Volume Filling Theory was proposed by Dubinin-Radushkevich and co-workers for adsorption from gas phase. It is related to Eucken/Polany'i potential theory (characteristic adsorption potential curve a = f(A) , where a is adsorption and A = RT ln(ps/p) is adsorption potential, and A=0 at saturation point; analogously, in solutions: A = RT ln(cs/c) ).
The DR isotherm describes adsorption on a single type of uniform pores (in this respect the DR isotherm is an analogue of Langmuir-like local isotherms in adsorption on energetically heterogeneous solids). In the case of simple systems, experimental isotherms may be described by e.g. bi-DR isotherm - corresponding to bimodal micropore system. This theory was later extended by Stoeckli in a manner analogous to the global integral equation used in adsorption on energetically heterogeneous solids, allowing it to describe a continuous distribution of pore sizes (or generally pore characteristics).
F - Freundlich (DA with n=1):
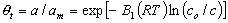
or in a more typical form:
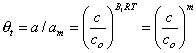
DR - Dubinin-Radushkevich (DA with n=2):
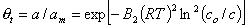
It is very often used in log-linear form
Exponential Jaroniec equation:
(A kind of virial equation for adsorption on microporous solids - F, DR and DA with integer exponent n values may be treated as special cases of this equation)
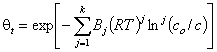
Stoeckli integral equation:
(Stoeckli equation describes adsorption in non-uniform micropores with distribution given by F(B) and B being a function of micropore size, B(r) )
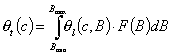
where usually local isotherm equation is Dubinin-Radushkevich eq., i.e. isotherm describing adsorption in spherical micropores of fixed pore size.
bi-DR (aka. Dubinin-Izotova) equation:
Bi-DR (aka. Dubinin-Izotova) equation may be considered a particular solution of Stoeckli equation with bimodal discrete pore distribution and adsorption on each pore type described by the Dubinin-Radushkevich equation:
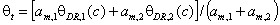
DS (Dubinin-Stoeckli) equation:
Dubinin-Stoeckli equation is a solution of Stoeckli equation for a gaussian pore distribution and adsorption on each pore type described by the Dubinin-Radushkevich equation:
Top
My papers
Search for papers
Main page
Send a message to Adam.Marczewski AT@AT umcs.lublin.pl