© A.W.Marczewski 2002
A Practical Guide to Isotherms of ADSORPTION on Heterogeneous Surfaces
Reload Adsorption Guide
Barret-Joyner-Halenda (BJH) calculation scheme
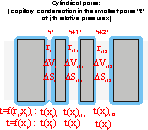
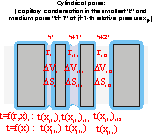
Barret-Joyner-Halenda scheme (1955) for calculation of mesopore distribution from nitrogen adsorption data may be summarized in the formula:
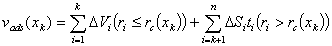
In this formula, vads(xk) is the volume of (liquid) adsorbate [cm3/g] at relative pressure xk (calculated from the value of adsorption expressed in [cm3/g STP] by vads(x) = 0.0015468 a(x) ), pore volume V is given in [cm3/g], S is surface area [m2/g] and t is the thickness of adsorbed layer (in appropriate units).
This formula says, that the adsorbed amount at k-th point of adsorption isoterm may be divided into 2 distinct parts:
1st is a volume in condensate in all pores smaller than some characteristic size depending on current relative pressure, rc(xk),
2nd is a volume of adsorbed film on all larger pores, calculated a sum of terms: Σ (pore surface) (thickness of film in pore).
NOTE!
One has to be always cautions as to identity of the radius used: in Kelvin equation xc = xc(r) and thickness equation t = t(x,r), radius is always determined by the menicus. However, in the calculation of ΔV and ΔS radius is a geometrical pore radius!
Pore radiuses should be calculated by Kelvin equation for a given pore model. The diameter of solid pore is a sum of meniscus diameter + 2 * thickness of adsorbed film. In general the thickness of adsorbed film depends not only on relative pressure (like for flat surface - e.g simple HJ and FHH equations) but also is affected by meniscus radius.
For a given pore with radius r (or diameter d - better for slit-shaped pores), the pore area and pore volume are related by simple geometric relations, e.g.:
for spherical pores: ΔV = d ΔS / 6
for cylinders: ΔV = d ΔS / 4
for slits: ΔV = d ΔS / 2.
For adsorption (condensation) and desorption (evaporation) isotherm branches the calculation scheme looks the same - you always start from the point where all pores are filled-up (i.e. last point of adsorption branch, xads,K where the adsorbed amount becomes the same as on desorption branch xdes,L) and - preferably - the pore system is (apparently) oversaturated. The last requirement is important if there is a possibility of existence of bottle-shaped pores. In practice it is always true. Then you go along decreasing pressure, i.e. you iterate isotherm point counter downwards (xads,i i = K, K-1, K-2 ... ) whereas for desorption upwards (xdes,i i = L, L+1, L+2 ...).
In the 1st step, the change of adsorbate amount corresponds to proesses in a single (averaged!) pore size. This pore size is calculated with appropriate form of Kelvin equation (meniscus) and equation defining the adsorbed film thickness for two limiting radiuses (corresponding to maximum, xi, and minimum, xi+1, pressure). In the following steps the information on all opened pores (i.e. ΔS(rj and ΔV(rj, j < i) is utilized.
E-mail addresses are modified to in order to prevent spamming / mail-abuse:
in e-mail remove spaces, replace " AT@AT " by "@"
Send a message to Adam.Marczewski AT@AT umcs.lublin.pl
Disclaimer