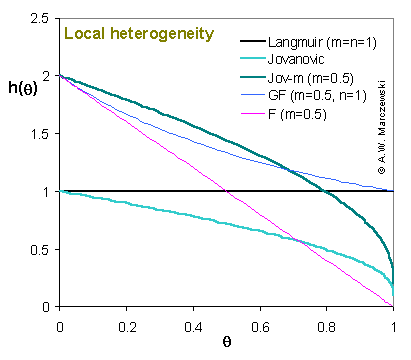
Local heterogeneity function, h(θ), for Jovanovic and Jovanovic-Freundlich (JF, aka. Jov-m, i.e. Jovanovic + heterogeneity) compared with Langmuir, Generalized Freundlich (GF)/Sips and Freundlich (F) equations.
© A.W.Marczewski 2002
A Practical Guide to Isotherms of ADSORPTION on Heterogeneous Surfaces
Global Heterogeneity, H:
local heterogeneity function h(θ): Jovanovic
(see global heterogeneity calc. plot)
Local heterogeneity function, h(θ), for Jovanovic and Jovanovic-Freundlich (JF, aka. Jov-m, i.e. Jovanovic + heterogeneity) compared with Langmuir, Generalized Freundlich (GF)/Sips and Freundlich (F) equations.
All equations (JF/Jov-m, GF and F) corresponding to heterogeneous surfaces and characterized by the same value of heterogeneity parameter m for low surface coverages θ behave in the same way :
hhet(θ → 0) = 1/m
However, for medium and high coverages θ) the differences become clear. For Freundlich and Jovanovic-derived isotherms:
hhet(θ → 1) = 0
as opposed to Langmuir-based GF isotherm:
(hGF(θ → 1) = hL(θ) = 1).
For other Langmuir-based isotherms (see model picture for GL): hGL(θ) ≥ hL(θ) = 1
Those differences result partially from their implied local isotherms, i.e. different adsorption/interaction models (Langmuir, Jovanovic, Freundlich), partially from the magnitude of heterogeneity effects (heterogeneous or homogeneous: JF (Jov-m) / Jov; GF / L) or shape of energy distribution function corresponding to apparently identical heterogeneity parameters or other factors (e.g. Freundlich should be used for weakly soluble substances with c ≤ cs).
For Freundlich equation point θ=1 corresponds to p=po , for other equations θ=1 is reached for p→∞ or [p/(1-x)]→∞ (for vapors x = p/ps and for weakly soluble solutes; x=c/cs).
NOTE.
Replace p with c for dilute solute adsorption.
Send a message to Adam.Marczewski AT@AT umcs.lublin.pl