ADSORPTION:LSQ data fitting (some ideas)
© A.W.Marczewski 2002
A Practical Guide to Isotherms of ADSORPTION on Heterogeneous Surfaces
ADSORPTION:
LSQ data fitting (some ideas)
Data Fit ( Blind / Advanced / Orthogonal / Data filtering )
Fitting Details 1 ( General Advice and tricks / Parameter specification )
Fitting Details 2 ( Multiple data sets / Relation of parameters )
Data Errors ( Data and error transformation / Data and fit simulation )
Outliers ( Robust optimization / Non-gaussian error distribution / Mistakes )
How to fit your adsorption isotherm data?
Data fitting/Optimisation
If you have no clues what to do next - use some data-fitting package and perform a blind fit first, but generally if you perform a blind fit with more than 2 parameters you'll have a "reasonable fit" for almost any adsorption data and isotherm equation!!!
Unless ...
Many fitting packages offer you an option of automatic selection of the fitting equation. Use it with caution. If you aim is just numerical description of data - doesn't matter what is the phenomenon behind it - you may even use polynomials. However, do not try to attribute any physicochemical meaning to that. Of course, many mathematical properties of your experimental isotherm may be later derived from such blind fit (e.g. smoothed isotherm and its derivatives may be used in order to find e.g. φ-function), but it is almost always better to use raw data in all data fitting.
Sometimes fitting packages offer you a separate option of data filtering. Such filtering should be used with caution if you intend to fit your data numerically. Usually it is better to use raw data in fitting/optimization, though for data presentation data filtering (e.g Savitzky-Golay) may be a great improvement. However, you must have lots and lots of data and usually approximately equally spaced. In specific situations you may also use Fourier or wavelet transforms as a means of adsorption data filtering. These methods may be especially useful in the analysis of kinetic adsorption or titration experiments.
Of course advanced fitting packages (you name them!) have ways of dealing with various problems, though even such a package works much more reliably if you feed it with a properly set-up problem.
So, some of you would like to say, why at all should I bother with anything more, e.g. data/error scaling/transformation etc., if I paid quite a money for something that should do (and usually it does) its work and fit my data nicely?
Of course you are generally right, but it is always proper to look at your data at various angles:
My general advice is: first try to reason out the type of adsorption model your data/system "should" fit, then try to guess/find etc. the range/set of equations (e.g. by a method below), finally - fit your data numerically, but watch out for problems - optimization is a tricky subject and you must know at least approximately what kind of experimental deviations you are getting - i.e. error distribution (Gaussian or not) and variation of deviations with experimental conditions. E.g. if std. deviation of Ads is constant - fit Ads; if std. deviation of Ads is proportional to Ads - fit log(Ads) etc. - see Data Transformation below. If your x,y data (or x,y,z-data etc.) has comparable errors/deviations of both x,y, then you need to perform Orthogonal Fitting. If you have many (at least apparent) outliers - you must consider outlier rejection and/or modification of LSq fitting or selection of other, more robust fitting method
A good trick is to change the way you specify your parameter and its' acceptable range. E.g. if you have to fit equilibrium constant K it is reasonable to use log(K) (range is -∞ to +∞) instead of K itself (range 0 to +∞) - the form of the parameter you choose for your optimising package (e.g MINUIT or even MS Excel) should give you approximately constant (or slowly changing) sensitivity of the fitted function to the parameter change. Of course, it is an additional overhead (log and exp functions) for your program, but increased stability is worth the cost.
Another gain is that your don't have problem with setting parameter limits (of course watch out for extremely small/large numbers) - your equilibrium constant that must always be non-zero positive - will always be - automatically, etc.
(BTW, many fitting packages routinely do similar tricks, however you can be smarter than the general purpose algorithm).
Depending on the isotherm and parameter (or sometimes the range of your data - eg. close to Henry region, or close to monolayer filling, etc.) you should try to find a right parameter form - parameter transform function (of course you should also fix your isotherms), e.g.:
θ = f(K,c) (you fit K)
should be transformed into:
θ = f(exp(lnK),c) (you fit lnK=ln(K)).
If you have e.g. several independently measured isotherms (e.g. for a series of temperatures) and your model allows you to predict at least a type of parameter change (e.g. par ~ T or par ~ 1/T etc.) (or - best - if your parameter stays constant), then you should optimise/LSq-fit all your data together. Of course you may try to fit individual isotherms separately - then you can see how poor is the correlation of your parameters with changing conditions (e.g. temperature).
Of course, it is always right to use a general idea of minimizing sum of scaled/weighted variances of your isotherms (with scaling/weighting factors related to the individual isotherm's best-fit variances):
Σwi (VARi) = Σwi (SDi)2
where the variance VAR for an individual isotherm (ni - no. of isotherm's points, k - no. of fitted parameters) is:
VARi = (SDi)2 = Σj [yexp,j - ytheor(xexp,j)]2 / (ni - k)
If the variances (or SD) of all isotherms and individual points are of the same order, and no. of experimental points measured for each isotherm is of the same order too, then you may take simply:
wi = ni
where ni is number of points in each isotherm. However, usually this is not the case.
This method in its orthodox form requires that you know in advance the variances - or calculate them from experimental data obtained by repetition of experiment is identical conditions.
However, in some cases a good idea - according to my experience (see e.g. A.Patrykiejew, M.Jaroniec and A.W.Marczewski: Chemica Scripta, 22, 136-145 (1983) or Thin Solid Films, 76, 247-258 (1981),
(doi). ) - is to minimize a product of individual isotherm standard deviations,
min { Π(SDi) }
or - equivalently - a product of variances (minimum is the same):
min { Π(VARi) } = min { Π(SDi)2 } ,
instead of usual sum of weighted variances (see above). This changes individual isotherm weight in the overall scheme - in a general LSq-fit a weight is proportional to the degrees of freedom of each data set. This is generally right - if the experimental variances of each experimental point are equal (quite rare) - especially if you compare measurements taken at distinctly different conditions (e.g. temperatures). However, in the above SD-product simplification, all isotherms in the overall fitting scheme have equal weight. The only thing that counts are the relative depths of isotherms' minima. Of course, if your separate isotherms have approximately equal no. of experimental points it doesn't change much.
An equivalent way is to use a sum of logarithms of respective isotherm deviations:
min { Σlog(VARi) }
or better with weights:
min { Σwi log(VARi) } .
In such a way only relative changes of individual isotherm's data deviations will have influence on global minimum (deeper minima will affect your optimisation more strongly than the shallow ones - independently on actual magnitude of any isotherm deviations) (of course, none of the VARi may be equal to zero). When compared with the general method, shallower minima may be obtained, i.e. a single very poorly fitted isotherm, or one very well fitted, have less influence on overall fit.
If the parameters of your isotherm series are not constant, but change with conditions and you know (or at least suspect) a general type of this dependence (e.g.: par(T) = A + B T, par(T) = A + B/T, log(par(T)) = A + B/T , etc.) then you may try to fit such line parameters (here A and B) instead of single, average paravg or a series of individual pari . Even if no. of parameters will grow (paravg vs. A and B), such an approach gives quite a good stability (unless given parameter changes very rapidly with conditions - in such a case continue reading). Additional gain may be such parameter dependence on conditions - if statistical analysis confirms it (or at least does not denies it).
Orthogonal fitting.
Very often, only one of your experimental isotherm a(c) variables is fitted (e.g. adsorption). It means, that you assume that the other one (concentration) is much more precisely measured. Even if it is generally true (though for strongly adsorbing solids, high initial concentration and small equilibrium concentration, your adsorption value will be calculated/measured more precisely than concentration), it is better to use a so-called orthogonal fitting where you take into account measurement errors for both variables. In such a case it is mandatory to use error weighting. Sometimes - instead of using error weighting one may use data transformation/scaling (see below). Here, a serious problem for such a simple version of orthogonal fitting is that it assumes that x,y errors are independent. E.g. for typical adsorption measurement, where we use material balance in order to find adsorption values, the errors of concentration measurement are "inherited" by adsorption values ( e.g.: a = (co - ceq)/m ). Then, it you fit your isotherm a(c), the deviations of adsorption, a, and concentration, c, are not independent.
Orthogonal fitting is also a good pick if you have more than 2 independently measured variables that all should fit some relation. You minimize sum of squares of distances (in n-dimensional space) of experimental points xn,exp(x1,exp,x2,exp,...,xn-1,exp) from some theoretically obtained curve xn(x1,x2,...,xn-1).
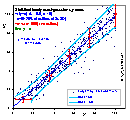
Data Transformation may be used instead of classic error weighting, if changing equation form transforms respective errors in such a way that these errors after transformation become constant. If orthogonal fitting is to be performed, then both axes may also be scaled in such a way, that we may attribute equal weight to such scaled x and y errors.
E.g., if err(x) is inversely proportional to x and err(y) is proportional to y:
err(x) ~ 1/x
err(y) ~ y
then data transformation may be the following:
x' = x2 and err(x')=const
y' = ln(y) and err(y')=const
If err(y) is a combination of constant error (e.g. background, signal noise etc.) and error proportional to magnitude of y, whereas the err(x) is approximately proportional to 1/x (but for x=0 the error is limited to some value resulting from background, b, or noise etc.) we may have (for x,y ≥ 0) e.g.:
err(x) ~ m/(x+b)
err(y) ~ (ky+a) = k(y + a/k)
then data transformation should be:
x' = (x + b)2 and err(x')=const
y' = ln(y + a/k) and err(y')=const
Generally, in order to obtain constant errors in the domains of transformed variables - err(x'), err(y') - you should transform your variables as follows:
x' = const(x') ∫ [1/err(x)] dx
y' = const(y') ∫ [1/err(y)] dy
where the values of const(x'), const(y') may be anything - if you fit with respect to a single variable (x' or y' only).
Of course (if x,y - and x', y' - are independent) in order to use orthogonal fitting without error weighting, some scaling of x' and y' is necessary - then const(x') and const(y') should be inversely proportional to x' and y' errors (SDx', SDx'), i.e.:
const(x') = 1/err(x')
const(y') = 1/err(y')
Now errors are constant and equal for both x' and y' and error weighting becomes "automatic" - it is embedded in x,y-data transformation. However, if no independent and reliable error estimates are available, it is still possible to obtain approximate estimates of such errors - or at least to make a rough guess. You may try to fit your data with respect to x-errors only, then y-errors only. Then, such obtained approximations of x and y standard deviations may serve as scaling factors for both axes (scale x by 1/SDx and y by 1/SDy).
If the dependence of x,y-data errors on magnitude of x,y is not so straightforward, we have to know more in order to "straighten" (i.e. scale) data errors, or treat data scaling/transformation only as a means to inspect your data in a more manageable form, most often linear. However, in some cases (e.g. linear Langmuir plot: a vs. a/c) data range is compacted in such a way, that in a single scale one may analyse the entire data range with approximately constant accuracy (another common compacting data transformation is log-log plot)
Sometimes the mathematical specific of data transformation requires the data remain strictly within some range, e.g. if you try linear DR relationship ( (-log θ)1/2 vs. log(c), where am must be estimated separately or LSq-fitted). If adsorption values are vary close to adsorption capacity, am, some of the points may have values slightly exceeding it (ai > am) due to natural experimental errors/deviations. If fitting procedure is protected againts root(negative) error, then such points - though in fact very close to the fitted line - will be rejected distorting your fit. In such a case it is better to allow such points to remain in the fit by slight modification of fitted variable: y = sign(-log θ) (|-log θ|)1/2 .
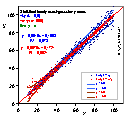
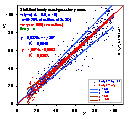Outliers are those experimental points that are farther from general population of experimental points, than it should - statistically - happen.
Outliers may affect very strongly your fitting results (even a single one) - even if the distribution of errors is strictly gaussian. In such a case rejection of outliers (discrete weighting correction - 0 or 1) or special weighting functions (smooth correction of weight - see above) that may lower statistical weight of outliers without their complete elimination (you newer know for sure if the rejected point is a "good" or "wrong" one - may be all other points are wrong an this one is OK - welcome to the reality of statistical deviations).
The reasons for the appearance of outliers may be of various nature:
Even the things that are not very probable, sometimes happen (compare some of Murhy's laws: "if sth may go wrong it does go wrong", or "in a computer program there is always one more error") - use some criterion for outlier rejection, e.g. 2.5σ. It results from simple analysis of Gaussian (i.e. normal) distribution of random errors, where the probabilities of finding the result in certain ranges (and equivalently, finding it outside such range is: 1-Prob) are:
Prob(xavg +/- σ) = 0.6826 - i.e. 32% of points outside this range
Prob(xavg +/- 2σ) = 0.9545 - only 5% of data outside this range
Prob(xavg +/- 2.5σ) = 0.9876 - only 1.25% (1 in 80) outside this range
Prob(xavg +/- 3σ) = 0.9973 - only 0.27% (i.e. 1 in 350) outside this range.
If you have eg. 100 experimental points, and if you have a single point (i.e. 1% of all 100 points) with deviation e.g. (yexp-ytheor) > 3σ then using the above you know that it may happen - statistically - but rejection of such an outlier is safer than leaving it. Even if some such points are basically within proper probability range it still may be safer to reject those that are farthest from your mean (or fitted line) on a "just in case" basis.
The error/deviation distribution is non-Gaussian, though still symmetrical - use more robust maximum likelihood estimators than variance, e.g.:
min { (1/n) Σ |yexp - ytheor| }
In the past this wasn't accepted by the majority of statisticians, however it has changed.
In order to know what kind of errors you are getting, you should repeat your whole experimental procedure many times (with exactly the same initial conditions) - then try to analyse error distribution function.
If error distribution is strongly asymmetrical, then the use of standard LSq optimization (which is a consequence of Gaussian distribution of errors - see below) may lead to grave fitting errors. In such a case you may still use standard method if you introduce appropriate error-ransformation function. Such a function should transform asymmetrical error distribution into Gaussian one.
Experimental mistake or experimental control problem - repeat experiment (if possible) and/or reject points (if obvious). If no. of points that qualify as outliers is too large, then you cannot reject all of them (population of experimental points should't be "decimated" by such an approach - you may loose some essential information if your analysis of data isn't quite right) - you should change statistical/fitting approach. Try other, more robust method of fitting (see above) adequate to the problem.
General conclusion is:
No matter how do you fit - if you know anything about your function or data - USE IT!
Data Fit ( Blind / Advanced / Orthogonal / Data filtering )
Fitting Details 1 ( General Advice and tricks / Parameter specification )
Fitting Details 2 ( Multiple data sets / Relation of parameters )
Data Errors ( Data and error transformation / Data and fit simulation )
Outliers ( Robust optimization / Non-gaussian error distribution / Mistakes )
My papers
Search for papers
Main page
Send a message to Adam.Marczewski AT@AT umcs.lublin.pl